Matemáticas: Trigonometría Numérica. Relaciones Trigonométricas.
La palabra "trigonometría"
significa "medición por triángulo".
Como se la presenta en muchos libros de texto, la trigonometría
incluye otros tópicos además de los triángulos
y medidas. Sin embargo, este capítulo del sitio es
sólo una introducción a los aspectos numéricos
de la trigonometría, relacionados con la medición
de longitudes y ángulos.
PROPIEDADES ESPECIALES DE LOS TRIÁNGULOS RECTÁNGULOS
Se ha definido el TRIANGULO RECTÁNGULO como todo triángulo
que contiene un ángulo recto. En un triángulo
rectángulo el lado opuesto al ánguo recto es
la HIPOTENUSA. (Ver figura 19-1.) En la figura 19-1 el lado
AC es la hipotenusa.
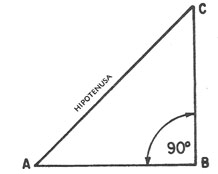
FIGURA 19-1. Triángulo rectángulo.
El filósofo griego Pitágoras descubrió
una importante propiedad de todos los triángulos rectángulos
que relaciona las longitudes de los tres lados.
TEOREMA DE PITÁGORAS
La regla o TEOREMA DE PITÁGORAS establece que el cuadrado
de la longitud de la hipotenusa (en todo triángulo
rectángulo) es igual a la suma de los cuadrados de
las longitudes de los otros dos lados.
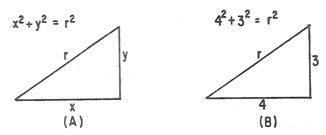
Figura 19-2. Teorema de Pitágoras.
(A) Triángulo general; (B) triángulo con lados
de longitudes específicas.
Por ejemplo, si los lados se designan como en la figura
19-2 (A), el teorema de Pitágoras se establece en símbolos
así:
x2 + y2 = r2
Esta propiedad la demostró Pitágoras para todos los triángulos
rectángulos.
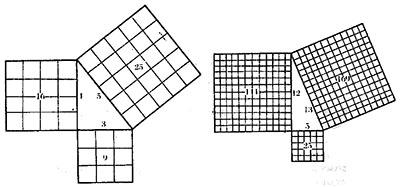
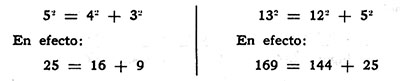
Figura : el cuadrado que tiene por lado la hipotenusa
tiene un área igual a la suma de las áreas de los cuadrados construidos sobre cada cateto, como se destaca en la figura.
He aquí un ejemplo del teorema de Pitágoras
en un problema:
EJEMPLO : Determinar la longitud de la
hipotenusa en el triángulo mostrado en la figura 19-2
(B).
SOLUCIÓN:
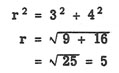
EJEMPLO: Un observador sobre un barco ubicado
en el punto A, figura 19-3, sabe que su distancia al punto
C es 1.200 m y que la longitud de BC es 1.300 m. Mide el ángulo
A y determina que es 90°. Calcular la distancia AB.
SOLUCIÓN: Por la regla de Pitágoras,
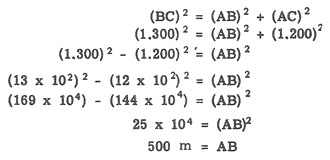
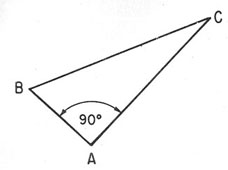
Figura 19-3. Empleo del teorema de Pitágoras.
Ejemplo : Un segmento de 15 cm de largo tiene una proyección de 12 cm sobre un eje, con el cual tiene un punto común, que es extremo del segmento. ¿A qué distancia del eje de proyección se encuentra el otro extremo del segmento?
Podemos abordar este problema utilizando el teorema de Pitágoras y la definición de proyección.
Sea "x" la distancia del otro extremo del segmento al eje de proyección. Luego, la proyección del segmento en el eje será de 12 cm. Dibujando un diagrama, podemos ver que el triángulo formado por el otro extremo del segmento, el punto de intersección del segmento con el eje de proyección y la proyección del segmento en el eje es un triángulo rectángulo.
Por lo tanto, podemos aplicar el teorema de Pitágoras para encontrar la longitud del otro lado del triángulo, que es la distancia que estamos buscando:
x² + 12² = 15²
x² = 225 - 144
x² = 81
x = √81
x = 9
Por lo tanto, el otro extremo del segmento está a una distancia de 9 cm del eje de proyección.
Ejemplo : Un segmento ha sido proyectado sobre un eje con el que forman un ángulo de 45°. Su proyección es de 14 cm. ¿Cuál es la longitud del segmento?
Podemos resolver este problema utilizando la definición de proyección y la trigonometría.
Sea "x" la longitud del segmento que estamos buscando. Luego, la proyección del segmento sobre el eje de proyección será igual a "x" multiplicado por el coseno del ángulo que forma con el eje de proyección. Como el ángulo formado es de 45°, podemos utilizar la propiedad de que el coseno de 45° es igual a la raíz cuadrada de 2 dividido por 2, es decir:
Proyección del segmento = x * cos(45°) = x * √2 / 2
Sabemos que la proyección del segmento es de 14 cm, por lo que podemos plantear la siguiente ecuación:
14 = x * √2 / 2
Multiplicando ambos lados por 2 / √2, obtenemos:
14 * 2 / √2 = x
Simplificando, obtenemos:
x = 28 / √2
Para simplificar aún más la expresión, podemos multiplicar el numerador y el denominador por √2:
x = 28 / √2 * √2 / √2
x = 28√2 / 2
x = 14√2
x ≈ 19.79
Por lo tanto, la longitud del segmento es de aproximadamente 19.79 cm.
Triángulos rectángulos
semejantes
Dos triángulos rectángulos son
SEMEJANTES si uno de los ángulos agudos del primero
es igual a uno de los ángulos agudos del segundo. Esta
conclusión se basa en los siguientes razonamientos:
1. El ángulo recto en el primer triángulo
es igual al ángulo recto en el segundo, puesto que
todos los ángulos rectos son iguales.
2. La suma de los ángulos de todo triángulo
es 180°. Por tanto, la suma de los dos ángulos
agudos en un triángulo rectángulo es 90°.
3. Representemos los ángulos agudos iguales de los
dos triángulos con A y A', respectivamente. (Ver figura
19-4) .Entonces, los otros ángulos agudos, B y B',
son como sigue:
B = 90° - A
B' = 90° - A'
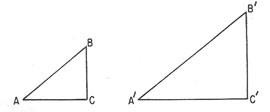
Figura 19-4. Triángulos rectángulos
semejantes.
4. Visto que los ángulos A y A' son iguales los ángulos
B y B' también son iguales.
5 . Deducimos que dos triángulos rectángulos
con uno de los ángulos agudos del primero igual a uno
de los ángulos agudos del segundo, tienen todos sus
ángulos correspondientes iguales.
Así pues, los dos triángulos son semejantes.
A menudo aparecen situaciones prácticas en las cuales
se emplean triángulos semejantes para resolver problemas.
Por ejemplo, la altura de un árbol puede determinarse
comparando la longitud de su sombra con la de un mástil
cercano, conforme se muestra en la figura 19-5.
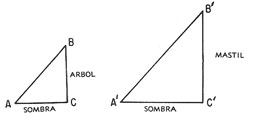
Figura 19-5. Cálculo de la altura por
comparación de las sombras.
Supongamos que los rayos del sol son paralelos
y que el árbol y el mástil forman ángulos
de 90° con la Tierra. Entonces, los triángulos
ABC y A'B'C' son triángulos rectángulos y el
ángulo B es igual al ángulo B'. Por consiguiente,
los triángulos son semejantes y sus lados correspondientes
son proporcionales, con el resultado que sigue:
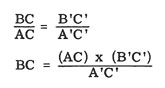
Supongamos que el mástil tiene 30 m de
altura, que la sombra del árbol es 12 m de largo y
que la sombra del mástil es 24 m de largo. En tal caso:
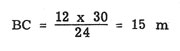
PRÁCTICA DE PROBLEMAS:
1, Un poste en la parte superior de una casa proyecta una
sombra de 48 m desde la base del edificio. Si el edificio
tiene 12 m de alto y su sombra es de 32 m, ¿cuál
es la longitud del poste? (Nota: Si la longitud del poste
es x, entonces la longitud de éste
sobre tierra es x + 12.)
2. La figura 19-6 representa un edificio en forma de L de
las dimensiones señaladas. Sobre la línea de
visión AD se coloca una estaca en C, un punto a 8 m
del edificio y a 10 m de A. Si ABC es el ángulo recto,
determinar la longitud de AB y AD. Observe que AE tiene 18
m y ED 24 m.
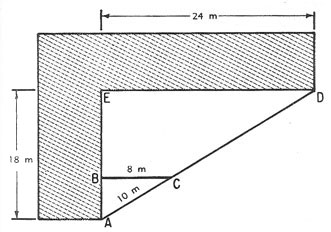
Figura 19-6. Empleo de triángulos semejantes.
Respuestas:
1. Si la longitud del poste sobre el edificio es "x", y la altura del edificio es de 12 metros, entonces la longitud total del poste (poste más la parte que está sobre el edificio) es de "x + 12".
La sombra del poste más el edificio en el piso es de 48 metros, y la sombra del edificio solo es de 32 metros. Entonces, la sombra de la parte del poste que se encuentra sobre el edificio es de 48 - 32 = 16 metros.
Ahora, podemos establecer la siguiente proporción:
(x + 12) / 16 = 12 / 32
donde 12 es la altura del edificio y 32 es la sombra del edificio.
Para despejar "x", podemos multiplicar ambos lados de la ecuación por 16:
x + 12 = 6
x = -6 + 12
x = 6
Por lo tanto, la longitud del poste sobre el edificio es de 6 metros, y la longitud total del poste y edificio es de 6 + 12 = 18 metros.
2. AB = 6 m AD = 30 m
RELACIONES TRIGONOMÉTRICAS
Las relaciones entre los ángulos y lados de los triángulos
rectángulos se expresan en términos de RELACIONES
TRIGONOMÉTRICAS. Por ejemplo, en la figura 19-7 los
lados del triángulo se denominan de acuerdo con sus
relaciones respecto del ángulo θ.
En trigonometría los ángulos se nombran generalmente
por medio de letras griegas. El nombre del símbolo θ es theta.
En la tabla 19-1 se han agrupado las seis relaciones trigonométricas
para el ángulo θ.
Las relaciones se definen como sigue:


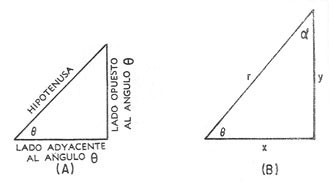
Figura 19-7. Relaciones entre los lados y ángulos
en un triángulo rectángulo. (A) Nombres de los
lados; (B) símbolos usados para designar los lados.
| Nombre de la relación |
Abreviatura |
| seno de θ |
sen θ |
| coseno de θ |
cos θ |
| tangente de θ |
tang θ |
| cotangente de θ |
cotg θ |
| secante de θ |
sec θ |
| cosecante de θ |
cosec θ |
Tabla 19-1. Relaciones trigonométricas
El otro ángulo agudo en la figura 19-7 (B) se designa
con α (letra griega alfa). El
lado opuesto de α es x y el lado adyacente de α es y.
Por tanto, las seis relaciones de α son como sigue:

Supongamos que los lados del triángulo
(B) en la figura 19-7 son: x = 3, y = 4, r = 5. En tal caso, cada una de las relaciones de los ángulos θ y α podrá
expresarse como una fracción común o como un
decimal, Por ejemplo:
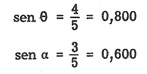
Se han calculado los valores decimales para las relaciones
de los ángulos entre 0° y 90° y los valores
para los ángulos por encima de 90° pueden expresarse
en términos de estos mismos valores por medio de fórmulas
de conversión. La secante, cosecante y cotangente,
cuando son necesarias, se calculan usando sus relaciones con
las tres relaciones principales. Estas son:

TRIANGULOS RECTANGULOS CON ANGULOS Y
RELACIONES ESPECIALES DE LADOS
Hay tres tipos de triángulos rectángulos
especialmente significativos por la frecuencia con que aparecen,
Ellos son los triángulos de 30°-60°-90°,
el de 45°-90° y el triángulo 3-4-5.
Triángulos de 30°-60°-90°
El triángulo de 30°-60°-90°
se llama así debido al tamaño de sus tres ángulos.
Los lados de este triángulo están en la relación
1 a √3 a 2, según se muestra en la figura
19-10.
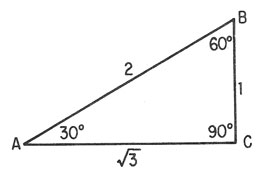
Figura 19-10. triángulo de 30°-60°-90°
La relación del seno para el ángulo
de 30° en la figura 19-10 establece los valores proporcionales
de los lados. Por ejemplo, sabemos que el seno dé 30°
es 1/2; por consiguiente, el lado AB debe tener el doble de
longitud que BC. Si el lado BC tiene 1 unidad de longitud,
entonces el lado AB posee 2 unidades de largo, y por la regla
de Pitágoras AC se determina como sigue:
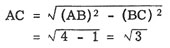
Independiente de la unidad de longitud, un triángulo
de 30°-60°-90° tiene una hipotenusa que es 2 veces
más larga que el lado más corto. El lado más
corto es opuesto al ángulo de 30°. El lado opuesto
al ángulo de 60° es √3 veces más largo
que el lado más corto. Por ejemplo, supongamos que
la hipotenusa de un triángulo de 30°-60°-90°
posee 30 unidades de longitud; entonces, el lado más
corto tiene 15 unidades y el lado opuesto al ángulo
de 60° tendrá 15 unidades.
PRÁCTICA DE PROBLEMAS:
Sin referirse a las tablas o al teorema de
Pitágoras, determine las siguientes longitudes y ángulos
en la figura 19-11:
| 1. Longitud de AC |
4. Longitud de RT |
| 2. Ángulo A |
5. Longitud de RS |
| 3. Ángulo B |
6. Ángulo T |
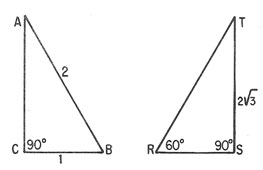
Figura 19-11. Determinación de elementos
en triángulos de 30°-60°-90°
| 1. √3 |
4. 4 |
| 2. 30° |
5. 2 |
| 3. 60° |
6. 30° |
Triángulo de 45°- 90°
La figura 19-12 ilustra un triángulo en el cual dos
ángulos miden 45° y el tercer ángulo mide
90°. Puesto que los ángulos A y B son iguales,
los lados opuestos a ellos también son iguales. Por
tanto, AC es igual a CB.
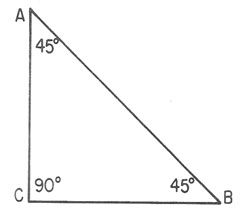
Figura 19-12. Triángulo de 45°
- 90°.
Supongamos que CB es 1 unidad de largo; entonces
AC también es 1 unidad de largo y la longitud de AB
se calcula de este modo:
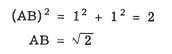
Independientemente del tamaño del triángulo,
si tiene dos ángulos de 45° y uno de 90° sus
lados están en la relación 1 a 1 a √2.
Por ejemplo, si los lados AC y CB poseen 3 unidades de largo,
AB tiene 3 √2 unidades de largo.
|